托勒密定理的证明是什么？

托勒密定理的证明是什么？

托勒密定理的证明是：

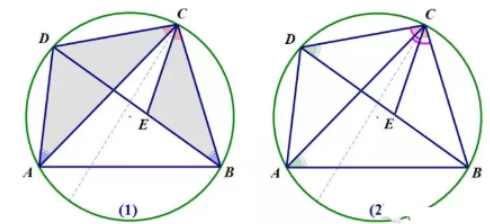
在任意凸四扮辩边形ABCD中（如右图），作△ABE使∠BAE=∠CAD∠ABE=∠ACD，连接DE

则△ABE∽△ACD

所以笑银BE/CD=AB/AC,即BE·AC=AB·CD

 (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD

所以△ABC∽△AED

BC/ED=AC/AD,即ED·AC=BC·AD (2)

(1)+(2),得

AC(BE+ED)=AB·CD+AD·BC

又因为BE+ED≥BD

（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）。

推论

1、任碰缺宴意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，当且仅当ABCD四点共圆时取等号。

2、托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。