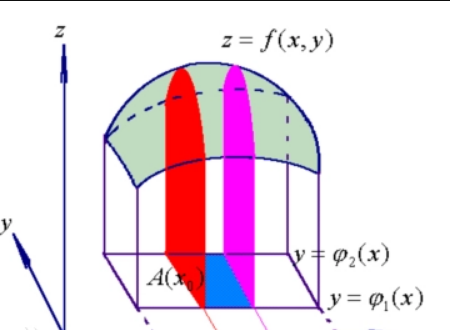
二重积分的几何意义

二重积分的几何意义

是一个曲面或者是理解成为一个无限分割的柱体或者是可以理解成为一个被积区域的质量。

在空间直角坐标系中，二重积分是各部分区域上柱体体积的代数和，在xoy平面上方的取正，在xoy平面下方的轮亩态取负。某些特殊的被积函数f（x，y）的所表示的曲面和D底面所为围的曲顶柱体的体积公式已知，可以用二重积分的几何意义的来计算。

二重积分详解：

二重积分是二元函数在空间上的积分腊源，同定积分类似，是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用，可以用来计算曲面的面积，平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的（有向）曲面上进行积分，称耐游为曲面积分。